Motion is a Lie - Zeno’s Paradox

Clap your hands once.

Now hold your hands one metre apart. Halve the distance between your hands. Halve it again. And again. Will your hands ever touch?

This is a very similar concept to one thought of by Zeno, a Greek philosopher over 2500 years ago. In his ‘Achilles and the Tortoise’ paradox, Zeno imagines a race between Achilles, the greatest Greek warrior, and a tortoise. In order to make the race slightly more balanced, the tortoise starts 100 metres ahead; when the race begins, Achilles sprints to the position the tortoise is at. But, of course, when Achilles reaches the tortoise's original position, the tortoise has moved some distance forward - let's say 10 metres. So now Achilles has to repeat his actions, sprinting to the new location of the tortoise, but again, by the time he reaches it, the tortoise has moved another metre forward. And so this continues, and as much as he tries, Achilles can never overtake the tortoise.

Zeno therefore claims that motion itself is impossible. In order to move to a point, you must first move to the halfway point, and the halfway point of that, and the halfway point of that … an infinite number of times. Zeno is, of course, incorrect; motion is definitely not impossible. The flaw in his argument is that he assumes the sum of an infinite number of distances must also be infinite, but we can prove this is not necessarily true.

Think back to the example of our hands. Starting with our hands one metre apart and halving the distance requires us to move our hands half of a metre, and halving again requires us to move our hands another quarter of a metre, and so on. We can write the total distance moved by our hands as an infinite sum…

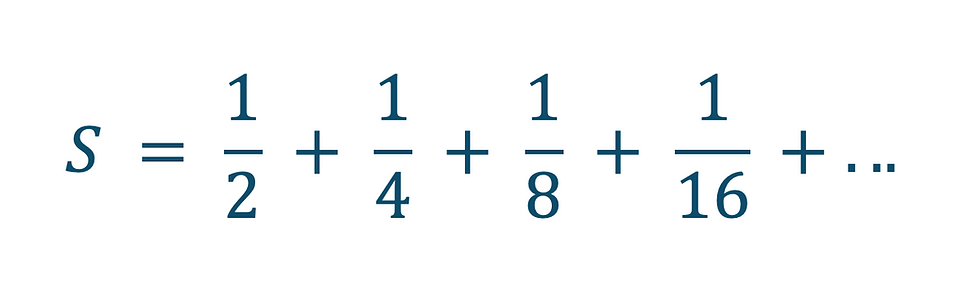
…and by halving this we get…

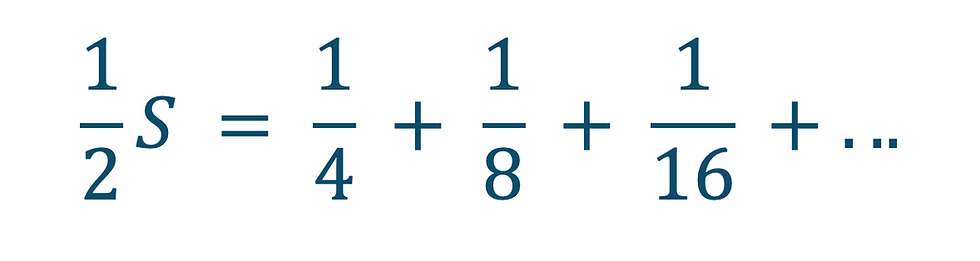
Subtracting the second sum from the first gives…

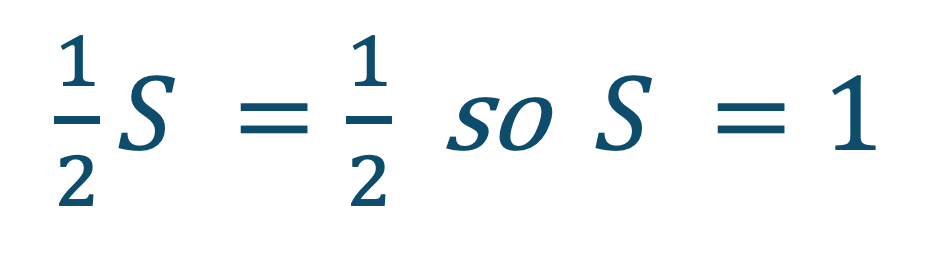
This implies that, even though we are moving our hands an infinite number of times, the total distance moved equals the one metre required for them to meet. This, while answering one question, raises another: how can an infinite process end?

Yes, by all real-world logic, Achilles can simply sprint past the tortoise immediately. Still, Zeno’s paradox challenges this simplicity, and while we know today that the sum of an infinite series is not necessarily infinite, it is still difficult to visualise why this is the case.

The unit triangle is a good way of visualising this problem. Via Pythagoras’s theorem, the hypotenuse of the unit triangle is √2, which is an irrational number. This means that it has an infinite number of non-repeating digits after the decimal point. Even so, we can still draw a line of length √2, and therefore an infinite sum of smaller and smaller distances can have a finite value.

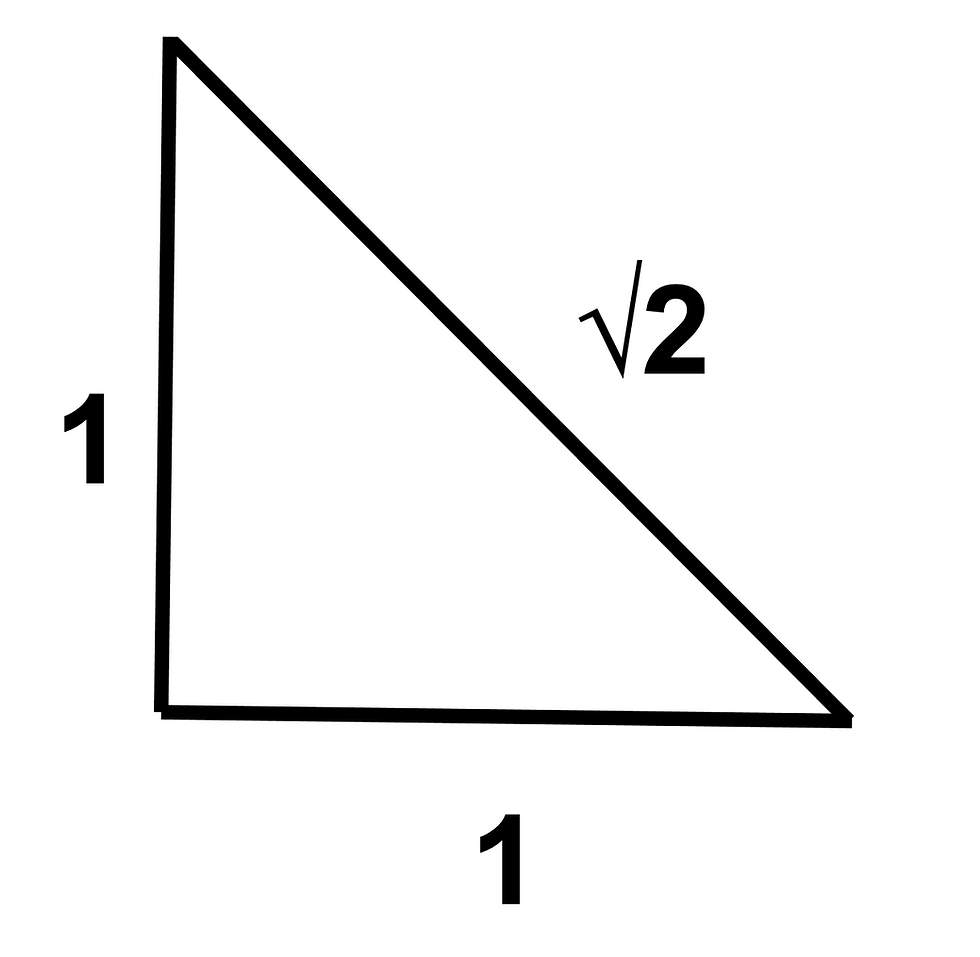
By unravelling the mysteries of Zeno's paradox, we are reminded that our understanding of the infinite continues to challenge and expand the boundaries of the reality we perceive.